1.1 복소평면
복소수를 기하학적으로 표현하기 위해 실수축과 허수축을 기반으로 한 평면.
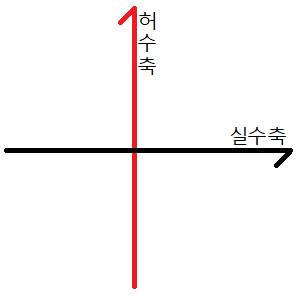
한 점을 나타날 때, (x, y) = x + y * i로 나타낸다. (x, y는 실수)
1.2 복소평면(2차원)에서의 회전
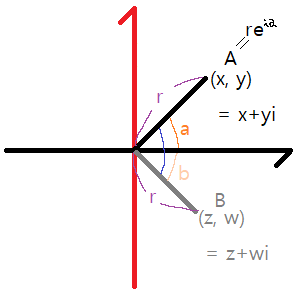
\(x = r × cos(a)\)
\(y = r × sin(a)\)
\(A = x + i × y = r × \bigl(cos(a) + i × sin(a)\bigr)\)
// 삼각함수 곱셈법칙
\(z = r × cos(a+b) = r × \bigl(cos(a) × cos(b) - sin(a) × sin(b)\bigr)\)
// 삼각함수 곱셈법칙
\(w = r × sin(a+b) = r × \bigl(sin(a) × cos(b) + cos(a) × sin(b)\bigr)\)
\(B = r × (z + i × w)\)
// -1을 \(i^2\) 로 변경
\({\scriptsize = r × \Bigl(cos(a) × cos(b) - sin(a) × sin(b) + i × \bigl(sin(a) × cos(b) + cos(a) × sin(b)\bigr)\Bigr)}\)
\({\scriptsize =r × \bigl(i^2 × sin(a) × sin(b) + i × sin(a) × cos(b) + i × cos(a) × sin(b) + cos(a) × cos(b)\bigr)}\)
// 곱셈공식 이용
\(\scriptsize = r × \Bigl(i × sin(a) × \bigl( i × sin(b) + cos(b)\bigr) + cos(a) × \bigl(i × sin(b) + cos(b)\bigr)\Bigr)\)
\(= r × \bigl(i × sin(a) + cos(a)\bigr) × \bigl(i × sin(b) + cos(b)\bigr)\)
=> 점 A에 회전복소수 \(\hat{v}=\bigl(cos(b), sin(b)\bigr)=cos(b)+sin(b)×i\)를 곱하게 되면 각도 b만큼 회전한 점 B를 얻게 된다는 것을 유도할 수 있고, 회전복소수 \(\hat{v}\)의 모습이 단위벡터와 같다는 점을 알 수 있다.
1.3 2차원 회전행렬
\(\left[\begin{matrix}cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta)\end{matrix}\right]\)
(수식 전개는 위키피디아의 회전변환행렬을 참고)
2.1 삼원수
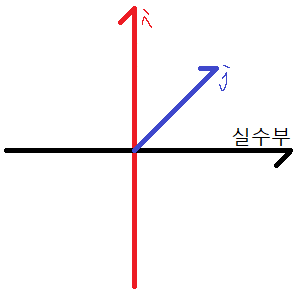
기본적으로 허수 i와 허수 j에 대하여 \(i^2 = j^2 = -1\)이다.
임의의 삼원수 A에 대하여 \(A = a + b × i + c × j (a, b, c는 실수)\)이다.
여기서 삼원수의 곱 중 하나인 \(i × j\)도 동일한 수 체계로 표현할 수 있어야 하므로 아래와 같이 나타낼 수 있다.
\(i × j = a + b × i + c × j\)
\(0 = a + b × i + c × j - i × j\)
\(0 = a + b × i + (c - i) × j\) or \(0 = a + (b - j) × i + c × j\)
\(a = 0, b = 0, c = i\) or \(a = 0, b = j, c = 0\)
여기서 전제조건 (a, b, c는 실수)를 만족시킬 수 없으므로 삼원수의 곱은 삼원수로 나타낼 수 없다는 사실을 알 수 있다.
곱셈이 잘 정의(well-defined)되어 있지 않기 때문에 수 체계라고 할 수 없다.
3.1 사원수(쿼터니온, Quaternion)
여기서 k라는 새로운 허수축을 도입하게 되면서 새로운 수 체계가 등장하게 된다.
사원수(쿼터니온, Quaternion)의 정의는 허수 i, 허수 j, 허수 k에 대하여 \(i^2 = j^2 = k^2 = i×j×k = -1\)이다.
이러한 성질을 이용하여 \(i×j = k, j × k = i, k × i = j\)도 유도가 가능하다.
다만 여기서 사원수는 곱셈에 대한 교환법칙이 성립하지 않는 다는 점(비가환)이 발견된다.
- \(i×j = k\) \(\neq\) \(j×i = k×i×i = -k\)
- \(k×i = j\) \(\neq\) \(i×k = i×i×j = -j\)
- \(j×k = i\) \(\neq\) \(k×j = i×j×j = -i\)
임의의 사원수 Q는 아래와 같이 표현한다.
\(Q = (w, x, y, z) = w + x × i + y × j + z × k (w, x, y, z는 실수)\)
임의의 사원수 Q에 대하여 실수부(스칼라부, w)와 허수부(벡터부, (x, y, z))로 나누는데 아래와 같은 표현도 가능하다.
\(v = (x, y, z)\)라 할 때, \(q = (w, v)\)이다.
3.2 사원수의 곱셈
\(Q_1 = a_1 + b_1i + c_1j + d_1k = (r_1, \vec{v_1})\)
\(Q_2 = a_2 + b_2i + c_2j + d_2k = (r_2, \vec{v_2})\)
\(\begin{align}Q_1Q_2 &= a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2\\ &+ (a_1b_2 + b_1a_2 + c_1d_2 - d_1c_2)i \\ &+ (a_1c_2 - b_1d_2 + c_1a_2 + d_1b_2)j \\ &+ (a_1d_2 + b_1c_2 - c_1b_2 + d_1a_2)k \\ &= (r_1r_2 - \vec{v_1}\cdot\vec{v_2}, r_1\vec{v_2} + r_2\vec{v_1} + \vec{v_1}×\vec{v_2}) \end{align}\)
3.3 3차원에서의 회전

점 P를 특정 축(\(\hat{v}\))을 이용해 \(\theta\)만큼 회전시킨 점 P'에 대한 공식은 아래와 같다.
\(P = (0, p)\)
\(P'=\hat{Q}P{\hat{Q}}^{-1}\)
연산에 사용할 회전 사원수 \(\hat{Q}\)는 크기가 1인 단위사원수이고 오일러공식을 만족시켜야 하는데
이는 실수부가 \(cos(\frac{\theta}{2})\)이고 허수부가 \(sin(\frac{\theta}{2})\)×단위벡터(Direction cosine, \(\hat{v}\))로 이루어져 있으며 아래와 같이 나타낼 수 있다.
\(\begin{align}\hat{Q} &= e^{\frac{\theta}{2}(v_xi+v_yj+v_zk)}\\ &= cos(\frac{\theta}{2}) + sin(\frac{\theta}{2})(v_xi+v_yj+v_zk) \\ &= (cos(\frac{\theta}{2}), sin(\frac{\theta}{2})×\hat{v})\end{align}\)
\(\begin{align}{\hat{Q}}^{-1} &= e^{\frac{\theta}{2}(v_xi+v_yj+v_zk)}\\ &= cos(\frac{\theta}{2}) - sin(\frac{\theta}{2})(v_xi+v_yj+v_zk) \\ &= (cos(\frac{\theta}{2}), -sin(\frac{\theta}{2})×\hat{v})\end{align}\)
연산은 로드리게스 회전 공식으로 귀결되는데 다음과 같이 표현할 수 있다.
\(P' = (0, p+w(v×p)+2(v×(v×p)))\)
3.4 3차원 회전 행렬
\(\left[\begin{matrix}1-2y^2-2z^2 & 2xy-2wz & 2xz+2wy & 0 \\ 2xy + 2wz & 1 - 2x^2 - 2z^2 & 2yz - 2wx & 0 \\ 2xz-2wy & 2yz + 2wx & 1 - 2x^2 -2y^2 & 0 \\ 0 & 0 & 0 & 1\end{matrix}\right]\)
마치며
켤레복소수(Complex conjurate)라던가, 항등원(Identity), 역원(Inverse), 노멀(Norm) 등에 대한 정리는 다른 분들의 포스팅에서 훨씬 잘 설명하고 있기 때문에 굳이 적지 않았다. 사실 시간이 된다면 로드리게스 회전 공식을 조금 더 파서 \(P'=\hat{Q}P{\hat{Q}}^{-1}\)를 위의 PPT와 링크와는 다른 방식으로 증명하고 싶은데 요 며칠 이것만 팠더니 머리가 아프다. 다른 일을 해야겠다.
References
복소평면
위키백과, 우리 모두의 백과사전. 복소평면에 나타낸 복소수 z와 켤레복소수의 기하학적 표현. 원점에서 점 z를 따라 그어진 파란색 선의 거리는 복소수 z의 절댓값을 나타내고 각 ¢은 z의 논의
ko.wikipedia.org
회전변환행렬
위키백과, 우리 모두의 백과사전. 둘러보기로 가기 검색하러 가기 좌표평면상에서 회전변환행렬을 응용한 폰트 그래픽의 회전(90º및 180º) 선형 변환에서 회전변환행렬(Rotation matrix)은 임의의 행
ko.wikipedia.org
Quaternions and spatial rotation - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Correspondence between quaternions and 3D rotations Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations o
en.wikipedia.org
쿼터니온(Quaternion) 정리
0. 왜? 고등학교때 렌더링 파이프라인에 대해서 배울 때, '...이렇게 x,y,z축 기준으로 돌아가는 회전 행렬들을 이용해서 회전 변환을 수행하면 축이 잠기는 짐벌락 현상이 일어나는데, 쿼터니온을
enghqii.tistory.com